Movimiento rectilíneo uniforme, es un movimiento en línea recta, en este tipo de movimientos la velocidad es constante y la aceleración es cero.
Emplearemos la ecuación 1.
Las coordenadas de posición las obtendremos integrando la
ecuación, cuando:
Esta ecuación se emplea solo cuando se sabe que la velocidad
de la partícula es constante.
Movimiento rectilíneo uniformemente acelerado, es cuando la
aceleración es constante, de la ecuación 2.
Si esta ecuación la sustituimos en la ecuación 1 se tiene:
Hemos obtenido ecuaciones en función del tiempo ahora obtendremos
una que no dependa del tiempo y esa es la ecuación 3.
Obtenemos tres ecuaciones cuando la aceleración es constante.
Que quede claro solo se pueden emplear si la aceleración
es constante, si no es constante se emplean las tres primeras.
Las primeras tres ecuaciones se emplean para todos los casos.
Las otras tes se emplean para aceleración constante.
Ejemplo. Un automóvil viaja a la derecha con una velocidad de
27 km/h, cuando se le aplica una aceleración constante a la izquierda de 9.81
m/s2. Explique que esta pasando en un intervalo de t=0 a t=5 seg.
aremos el diagrama.
Usaremos las ecuaciones de aceleración constante. Para ello tenemos
que darlas de alta y esto se logra con la indicación en rojo.
Que posición y velocidad tendrá el móvil en 5 seg.
La velocidad en 5 seg.
Como sabemos la posición en 5 seg que es de x5 = 72.625 m.
Para variar hacemos otro diagrama.
Cuanto tarda en detenerse y que posición ocupa.
Dos formad y un mismo resultado.
A partir de la posición x1 el vehículo empieza a regresar.
Cuanto tiempo tarda en regresar de la posición x1
a posición xo y que velocidad tendrá.
Tiempo desde que sale de la posición xo y
regresa a la posición xo.
Otra forma es sumando los tiempos t0-1=1.019
seg y t1-0=1.019 seg.
Si tenemos un tiempo total de 5 seg y le restamos el tiempo t0-0=2.038
seg nos queda t0´-5= 2.962 seg. Con este tiempo determina la posición
y la velocidad.
¿Por qué nos dio un signo positivo?
Nos volvió a dar positivo, que está pasando.
Ahora de este problema determina la velocidad y el tiempo
en la posición xA = 4 m y la posición en xB = -40 m. (¿por
qué en xB se pone el signo negativo?).
No dio dos tiempos cual es el correcto.
Velocidad en xA primer tiempo.
Observa y compara los resultados.
Para no dejarlo, determinamos la velocidad con el segundo tiempo.
Con un tiempo mayor de 1.019 seg yo supongo que la velocidad va de regreso.
¿Qué está pasando? No dio un signo negativo.
Con este nuevo diagrama, noto que la partícula pasa dos veces
por el mismo punto, uno de ida y otro de regresa.
Esta nueva información no ayuda a darle la interpretación correcta
a la ecuación que se empleara.
Ahora nos quedó positiva, que significa.
Para este tipo de problemas el signo positivo nos indica que
la observación que se hace es correcta e incorrecta si nos da negativo.
(en la posición velocidad y aceleración el signo positivo nos
indica que la suposición es correcta).
La velocidad y el tiempo en la posición xB
= -40 m.
Un nuevo diagrama con la información que tenemos.
Para la posición xA pasa dos veces y una vez para
la posición xB. No se te olvide la referencia en rojo.
Nos quedamos con el signo positivo.
Los temas que se acaban de ver son caída libre, tiro vertical.


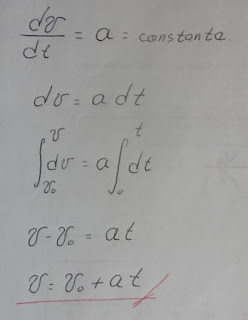



















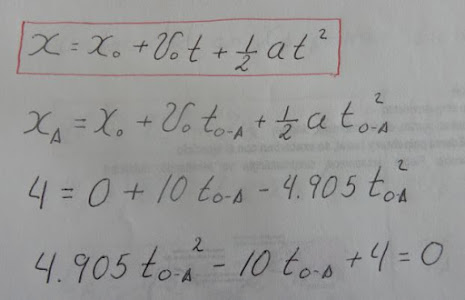









No hay comentarios:
Publicar un comentario