El movimiento curvilíneo se presenta cuando la partícula se mueve a lo largo de una trayectoria curva.
La ecuación de la velocidad es:
Emplearemos las coordenadas cartesianas.
El problema del proyectil es el ejemplo clásico.
Tendremos las componentes rectangulares de los vectores de
posición, velocidad y aceleración del proyectil
Coordenadas cartesianas.
Movimiento de un proyectil.
Esta forma muy común de movimiento se analiza tomando en
cuenta las siguientes condiciones, ideales y sin ninguna perdida.
El movimiento se realiza en un plano.
1. Recomendamos que el movimiento lo dividamos en dos, uno horizontal
y otro vertical.
2. El eje vertical es donde actúa la gravedad que seria
nuestra aceleración y la consideramos constante y siempre apunta al centro de
la tierra.
3.-En el eje vertical el movimiento se considera a velocidad
constante, puesto que la gravedad no lo afecta.
4.- La velocidad se proyecta sobre los ejes horizontal y
vertical.
5.- Lo que tiene en común estos dos movimientos aparentemente
independientes es el tiempo. El tiempo es lo que une estas ecuaciones.
Trayectorias parabólicas de un proyectil que parte del
origen.
Ecuaciones que se emplean.
Emplearemos las ecuaciones de aceleración constante la cuales
se tiene que adaptar al caso que se analiza.
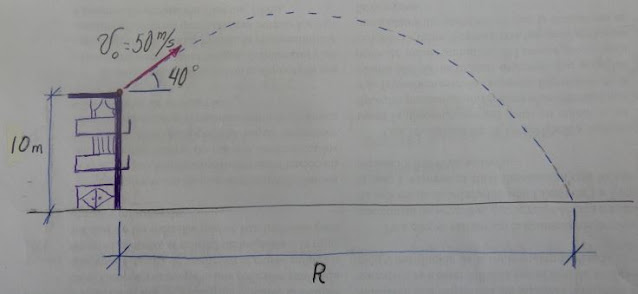
Desde el borde de una casa de 10 m de altura se dispara un
proyectil, con una velocidad de 50 m/s y un ángulo de 40o sobre el
horizonte, a que distancia del edificio golpeara el proyectil.
El alcance máximo lo obtenemos. Movimiento horizontal.
Movimiento horizontal.
¿Qué más puedes encontrar de este problema?
(solo tu decides si prácticas, es tu responsabilidad adquirir
nuevos conocimientos y ponerlos en práctica).
Despreciando la resistencia del aire, determine el valor del
ángulo de disparo para que el proyectil golpee el punto B.
Movimiento horizontal.
Movimiento vertical.
Sustituimos el tiempo.
Identidad trigonométrica.
Tenemos dos ángulos que golpearan en el punto B.





















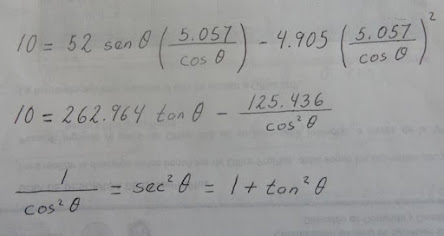


No hay comentarios:
Publicar un comentario